Minimal Perfect Hash Functions - Introduction
Basic Concepts
Suppose  is a universe of keys.
Let
is a universe of keys.
Let  be a hash function that maps the keys from
be a hash function that maps the keys from  to a given interval of integers
to a given interval of integers  .
Let
.
Let 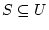 be a set of
be a set of  keys from
keys from  .
Given a key
.
Given a key  , the hash function
, the hash function  computes an
integer in
computes an
integer in  for the storage or retrieval of
for the storage or retrieval of  in
a hash table.
Hashing methods for non-static sets of keys can be used to construct
data structures storing
in
a hash table.
Hashing methods for non-static sets of keys can be used to construct
data structures storing  and supporting membership queries
"
and supporting membership queries
" ?" in expected time
?" in expected time  .
However, they involve a certain amount of wasted space owing to unused
locations in the table and waisted time to resolve collisions when
two keys are hashed to the same table location.
.
However, they involve a certain amount of wasted space owing to unused
locations in the table and waisted time to resolve collisions when
two keys are hashed to the same table location.
For static sets of keys it is possible to compute a function
to find any key in a table in one probe; such hash functions are called
perfect.
More precisely, given a set of keys  , we shall say that a
hash function
, we shall say that a
hash function  is a perfect hash function
for
is a perfect hash function
for  if
if  is an injection on
is an injection on  ,
that is, there are no collisions among the keys in
,
that is, there are no collisions among the keys in  :
if
:
if  and
and 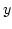 are in
are in  and
and  ,
then
,
then  .
Figure 1(a) illustrates a perfect hash function.
Since no collisions occur, each key can be retrieved from the table
with a single probe.
If
.
Figure 1(a) illustrates a perfect hash function.
Since no collisions occur, each key can be retrieved from the table
with a single probe.
If  , that is, the table has the same size as
, that is, the table has the same size as  ,
then we say that
,
then we say that  is a minimal perfect hash function
for
is a minimal perfect hash function
for  .
Figure 1(b) illustrates a minimal perfect hash function.
Minimal perfect hash functions totally avoid the problem of wasted
space and time. A perfect hash function
.
Figure 1(b) illustrates a minimal perfect hash function.
Minimal perfect hash functions totally avoid the problem of wasted
space and time. A perfect hash function  is order preserving
if the keys in
is order preserving
if the keys in  are arranged in some given order
and
are arranged in some given order
and  preserves this order in the hash table.
preserves this order in the hash table.
 |
| Figure 1: (a) Perfect hash function. (b) Minimal perfect hash function. |
Minimal perfect hash functions are widely used for memory efficient
storage and fast retrieval of items from static sets, such as words in natural
languages, reserved words in programming languages or interactive systems,
universal resource locations (URLs) in Web search engines, or item sets in
data mining techniques.
Enjoy!
Davi de Castro Reis
Djamel Belazzougui
Fabiano Cupertino Botelho
Nivio Ziviani

 is a universe of keys.
Let
is a universe of keys.
Let  be a hash function that maps the keys from
be a hash function that maps the keys from  to a given interval of integers
to a given interval of integers  .
Let
.
Let 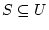 be a set of
be a set of  keys from
keys from  .
Given a key
.
Given a key  , the hash function
, the hash function  computes an
integer in
computes an
integer in  for the storage or retrieval of
for the storage or retrieval of  in
a hash table.
Hashing methods for non-static sets of keys can be used to construct
data structures storing
in
a hash table.
Hashing methods for non-static sets of keys can be used to construct
data structures storing  and supporting membership queries
"
and supporting membership queries
" ?" in expected time
?" in expected time  .
However, they involve a certain amount of wasted space owing to unused
locations in the table and waisted time to resolve collisions when
two keys are hashed to the same table location.
.
However, they involve a certain amount of wasted space owing to unused
locations in the table and waisted time to resolve collisions when
two keys are hashed to the same table location.
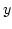 are in
are in  ,
then
,
then  .
Figure 1(a) illustrates a perfect hash function.
Since no collisions occur, each key can be retrieved from the table
with a single probe.
If
.
Figure 1(a) illustrates a perfect hash function.
Since no collisions occur, each key can be retrieved from the table
with a single probe.
If  , that is, the table has the same size as
, that is, the table has the same size as 