BMZ Algorithm
History
At the end of 2003, professor Nivio Ziviani was
finishing the second edition of his book.
During the book writing,
professor Nivio Ziviani studied the problem of generating
minimal perfect hash functions
(if you are not familiarized with this problem, see [1][2]).
Professor Nivio Ziviani coded a modified version of
the CHM algorithm, which was proposed by
Czech, Havas and Majewski, and put it in his book.
The CHM algorithm is based on acyclic random graphs to generate
order preserving minimal perfect hash functions in linear time.
Professor Nivio Ziviani
argued himself, why must the random graph
be acyclic? In the modified version availalbe in his book he got rid of this restriction.
The modification presented a problem, it was impossible to generate minimal perfect hash functions
for sets with more than 1000 keys.
At the same time, Fabiano C. Botelho,
a master degree student at Departament of Computer Science in
Federal University of Minas Gerais,
started to be advised by Nivio Ziviani who presented the problem
to Fabiano.
During the master, Fabiano and
Nivio Ziviani faced lots of problems.
In april of 2004, Fabiano was talking with a
friend of him (David Menoti) about the problems
and many ideas appeared.
The ideas were implemented and a very fast algorithm to generate
minimal perfect hash functions had been designed.
We refer the algorithm to as BMZ, because it was conceived by Fabiano C. Botelho,
David Menoti and Nivio Ziviani. The algorithm is described in [1].
To analyse BMZ algorithm we needed some results from the random graph theory, so
we invited professor Yoshiharu Kohayakawa to help us.
The final description and analysis of BMZ algorithm is presented in [2].
The Algorithm
The BMZ algorithm shares several features with the CHM algorithm.
In particular, BMZ algorithm is also
based on the generation of random graphs  , where
, where  is in
one-to-one correspondence with the key set
is in
one-to-one correspondence with the key set  for which we wish to
generate a minimal perfect hash function.
The two main differences between BMZ algorithm and CHM algorithm
are as follows: (i) BMZ algorithm generates random
graphs
for which we wish to
generate a minimal perfect hash function.
The two main differences between BMZ algorithm and CHM algorithm
are as follows: (i) BMZ algorithm generates random
graphs  with
with  and
and  , where
, where  ,
and hence
,
and hence  necessarily contains cycles,
while CHM algorithm generates acyclic random
graphs
necessarily contains cycles,
while CHM algorithm generates acyclic random
graphs  with
with  and
and  ,
with a greater number of vertices:
,
with a greater number of vertices:  ;
(ii) CHM algorithm generates order preserving minimal perfect hash functions
while BMZ algorithm does not preserve order. Thus, BMZ algorithm improves
the space requirement at the expense of generating functions that are not
order preserving.
;
(ii) CHM algorithm generates order preserving minimal perfect hash functions
while BMZ algorithm does not preserve order. Thus, BMZ algorithm improves
the space requirement at the expense of generating functions that are not
order preserving.
Suppose  is a universe of keys.
Let
is a universe of keys.
Let 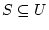 be a set of
be a set of  keys from
keys from  .
Let us show how the BMZ algorithm constructs a minimal perfect hash function
.
Let us show how the BMZ algorithm constructs a minimal perfect hash function  .
We make use of two auxiliary random functions
.
We make use of two auxiliary random functions  and
and  ,
where
,
where  for some suitably chosen integer
for some suitably chosen integer  ,
where
,
where  .We build a random graph
.We build a random graph  on
on  ,
whose edge set is
,
whose edge set is  . There is an edge in
. There is an edge in  for each
key in the set of keys
for each
key in the set of keys  .
.
In what follows, we shall be interested in the 2-core of
the random graph  , that is, the maximal subgraph
of
, that is, the maximal subgraph
of  with minimal degree at
least 2 (see [2] for details).
Because of its importance in our context, we call the 2-core the
critical subgraph of
with minimal degree at
least 2 (see [2] for details).
Because of its importance in our context, we call the 2-core the
critical subgraph of  and denote it by
and denote it by  .
The vertices and edges in
.
The vertices and edges in  are said to be critical.
We let
are said to be critical.
We let  and
and  .
Moreover, we let
.
Moreover, we let  be the set of non-critical
vertices in
be the set of non-critical
vertices in  .
We also let
.
We also let  be the set of all critical
vertices that have at least one non-critical vertex as a neighbour.
Let
be the set of all critical
vertices that have at least one non-critical vertex as a neighbour.
Let  be the set of non-critical edges in
be the set of non-critical edges in  .
Finally, we let
.
Finally, we let  be the non-critical subgraph
of
be the non-critical subgraph
of  .
The non-critical subgraph
.
The non-critical subgraph  corresponds to the acyclic part
of
corresponds to the acyclic part
of  .
We have
.
We have  .
.
We then construct a suitable labelling  of the vertices
of
of the vertices
of  : we choose
: we choose  for each
for each  in such
a way that
in such
a way that  (
( ) is a
minimal perfect hash function for
) is a
minimal perfect hash function for  .
This labelling
.
This labelling  can be found in linear time
if the number of edges in
can be found in linear time
if the number of edges in  is at most
is at most  (see [2]
for details).
(see [2]
for details).
Figure 1 presents a pseudo code for the BMZ algorithm.
The procedure BMZ ( ,
,  ) receives as input the set of
keys
) receives as input the set of
keys  and produces the labelling
and produces the labelling  .
The method uses a mapping, ordering and searching approach.
We now describe each step.
.
The method uses a mapping, ordering and searching approach.
We now describe each step.
procedure BMZ ( , ,  ) ) |
Mapping ( , ,  ); ); |
Ordering ( , ,  , ,  ); ); |
Searching ( , ,  , ,  , ,  ); ); |
| Figure 1: Main steps of BMZ algorithm for constructing a minimal perfect hash function |
Mapping Step
The procedure Mapping ( ,
,  ) receives as input the set
of keys
) receives as input the set
of keys  and generates the random graph
and generates the random graph  , by generating
two auxiliary functions
, by generating
two auxiliary functions  ,
,  .
.
The functions  and
and  are constructed as follows.
We impose some upper bound
are constructed as follows.
We impose some upper bound  on the lengths of the keys in
on the lengths of the keys in  .
To define
.
To define  (
( ,
,  ), we generate
an
), we generate
an  table of random integers
table of random integers  .
For a key
.
For a key  of length
of length  and
and  , we let
, we let
The random graph  has vertex set
has vertex set  and
edge set
and
edge set  . We need
. We need  to be
simple, i.e.,
to be
simple, i.e.,  should have neither loops nor multiple edges.
A loop occurs when
should have neither loops nor multiple edges.
A loop occurs when  for some
for some  .
We solve this in an ad hoc manner: we simply let
.
We solve this in an ad hoc manner: we simply let  in this case.
If we still find a loop after this, we generate another pair
in this case.
If we still find a loop after this, we generate another pair  .
When a multiple edge occurs we abort and generate a new pair
.
When a multiple edge occurs we abort and generate a new pair  .
Although the function above causes collisions with probability 1/t,
in cmph library we use faster hash
functions (DJB2 hash, FNV hash,
Jenkins hash and SDBM hash)
in which we do not need to impose any upper bound
.
Although the function above causes collisions with probability 1/t,
in cmph library we use faster hash
functions (DJB2 hash, FNV hash,
Jenkins hash and SDBM hash)
in which we do not need to impose any upper bound  on the lengths of the keys in
on the lengths of the keys in  .
.
As mentioned before, for us to find the labelling  of the
vertices of
of the
vertices of  in linear time,
we require that
in linear time,
we require that  .
The crucial step now is to determine the value
of
.
The crucial step now is to determine the value
of  (in
(in  ) to obtain a random
graph
) to obtain a random
graph  with
with  .
Botelho, Menoti an Ziviani determinded emprically in [1] that
the value of
.
Botelho, Menoti an Ziviani determinded emprically in [1] that
the value of  is 1.15. This value is remarkably
close to the theoretical value determined in [2],
which is around
is 1.15. This value is remarkably
close to the theoretical value determined in [2],
which is around  .
.
Ordering Step
The procedure Ordering ( ,
,  ,
,  ) receives
as input the graph
) receives
as input the graph  and partitions
and partitions  into the two
subgraphs
into the two
subgraphs  and
and  , so that
, so that  .
.
Figure 2 presents a sample graph with 9 vertices
and 8 edges, where the degree of a vertex is shown besides each vertex.
Initially, all vertices with degree 1 are added to a queue  .
For the example shown in Figure 2(a),
.
For the example shown in Figure 2(a),  after the initialization step.
after the initialization step.
 |
| Figure 2: Ordering step for a graph with 9 vertices and 8 edges. |
Next, we remove one vertex  from the queue, decrement its degree and
the degree of the vertices with degree greater than 0 in the adjacent
list of
from the queue, decrement its degree and
the degree of the vertices with degree greater than 0 in the adjacent
list of  , as depicted in Figure 2(b) for
, as depicted in Figure 2(b) for  .
At this point, the adjacencies of
.
At this point, the adjacencies of  with degree 1 are
inserted into the queue, such as vertex 1.
This process is repeated until the queue becomes empty.
All vertices with degree 0 are non-critical vertices and the others are
critical vertices, as depicted in Figure 2(c).
Finally, to determine the vertices in
with degree 1 are
inserted into the queue, such as vertex 1.
This process is repeated until the queue becomes empty.
All vertices with degree 0 are non-critical vertices and the others are
critical vertices, as depicted in Figure 2(c).
Finally, to determine the vertices in  we collect all
vertices
we collect all
vertices  with at least one vertex
with at least one vertex  that
is in Adj
that
is in Adj and in
and in  , as the vertex 8 in Figure 2(c).
, as the vertex 8 in Figure 2(c).
Searching Step
In the searching step, the key part is
the perfect assignment problem: find  such that
the function
such that
the function  defined by
defined by
is a bijection from  to
to  (recall
(recall  ).
We are interested in a labelling
).
We are interested in a labelling  of
the vertices of the graph
of
the vertices of the graph  with
the property that if
with
the property that if  and
and 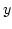 are keys
in
are keys
in  , then
, then  ; that is, if we associate
to each edge the sum of the labels on its endpoints, then these values
should be all distinct.
Moreover, we require that all the sums
; that is, if we associate
to each edge the sum of the labels on its endpoints, then these values
should be all distinct.
Moreover, we require that all the sums  (
( )
fall between
)
fall between  and
and  , and thus we have a bijection
between
, and thus we have a bijection
between  and
and  .
.
The procedure Searching ( ,
,  ,
,  ,
,  )
receives as input
)
receives as input  ,
,  ,
,  and finds a
suitable
and finds a
suitable  bit value for each vertex
bit value for each vertex  , stored in the
array
, stored in the
array  .
This step is first performed for the vertices in the
critical subgraph
.
This step is first performed for the vertices in the
critical subgraph  of
of  (the 2-core of
(the 2-core of  )
and then it is performed for the vertices in
)
and then it is performed for the vertices in  (the non-critical subgraph
of
(the non-critical subgraph
of  that contains the "acyclic part" of
that contains the "acyclic part" of  ).
The reason the assignment of the
).
The reason the assignment of the  values is first
performed on the vertices in
values is first
performed on the vertices in  is to resolve reassignments
as early as possible (such reassignments are consequences of the cycles
in
is to resolve reassignments
as early as possible (such reassignments are consequences of the cycles
in  and are depicted hereinafter).
and are depicted hereinafter).
Assignment of Values to Critical Vertices
The labels  (
( )
are assigned in increasing order following a greedy
strategy where the critical vertices
)
are assigned in increasing order following a greedy
strategy where the critical vertices  are considered one at a time,
according to a breadth-first search on
are considered one at a time,
according to a breadth-first search on  .
If a candidate value
.
If a candidate value  for
for  is forbidden
because setting
is forbidden
because setting  would create two edges with the same sum,
we try
would create two edges with the same sum,
we try  for
for  . This fact is referred to
as a reassignment.
. This fact is referred to
as a reassignment.
Let  be the set of addresses assigned to edges in
be the set of addresses assigned to edges in  .
Initially
.
Initially  .
Let
.
Let  be a candidate value for
be a candidate value for  .
Initially
.
Initially  .
Considering the subgraph
.
Considering the subgraph  in Figure 2(c),
a step by step example of the assignment of values to vertices in
in Figure 2(c),
a step by step example of the assignment of values to vertices in  is
presented in Figure 3.
Initially, a vertex
is
presented in Figure 3.
Initially, a vertex  is chosen, the assignment
is chosen, the assignment  is made
and
is made
and  is set to
is set to  .
For example, suppose that vertex
.
For example, suppose that vertex  in Figure 3(a) is
chosen, the assignment
in Figure 3(a) is
chosen, the assignment  is made and
is made and  is set to
is set to  .
.
 |
| Figure 3: Example of the assignment of values to critical vertices. |
In Figure 3(b), following the adjacent list of vertex  ,
the unassigned vertex
,
the unassigned vertex  is reached.
At this point, we collect in the temporary variable
is reached.
At this point, we collect in the temporary variable  all adjacencies
of vertex
all adjacencies
of vertex  that have been assigned an
that have been assigned an  value,
and
value,
and  .
Next, for all
.
Next, for all  , we check if
, we check if  .
Since
.
Since  , then
, then  is set
to
is set
to  ,
,  is incremented
by 1 (now
is incremented
by 1 (now  ) and
) and  .
Next, vertex
.
Next, vertex  is reached,
is reached,  is set
to
is set
to  ,
,  is set to
is set to  and
and  .
Next, vertex
.
Next, vertex  is reached and
is reached and  .
Since
.
Since  and
and  , then
, then  is
set to
is
set to  ,
,  is set to
is set to  and
and  .
Finally, vertex
.
Finally, vertex  is reached and
is reached and  .
Since
.
Since  ,
,  is incremented by 1 and set to 5, as depicted in
Figure 3(c).
Since
is incremented by 1 and set to 5, as depicted in
Figure 3(c).
Since  ,
,  is again incremented by 1 and set to 6,
as depicted in Figure 3(d).
These two reassignments are indicated by the arrows in Figure 3.
Since
is again incremented by 1 and set to 6,
as depicted in Figure 3(d).
These two reassignments are indicated by the arrows in Figure 3.
Since  and
and  , then
, then  is set
to
is set
to  and
and  . This finishes the algorithm.
. This finishes the algorithm.
Assignment of Values to Non-Critical Vertices
As  is acyclic, we can impose the order in which addresses are
associated with edges in
is acyclic, we can impose the order in which addresses are
associated with edges in  , making this step simple to solve
by a standard depth first search algorithm.
Therefore, in the assignment of values to vertices in
, making this step simple to solve
by a standard depth first search algorithm.
Therefore, in the assignment of values to vertices in  we
benefit from the unused addresses in the gaps left by the assignment of values
to vertices in
we
benefit from the unused addresses in the gaps left by the assignment of values
to vertices in  .
For that, we start the depth-first search from the vertices in
.
For that, we start the depth-first search from the vertices in  because
the
because
the  values for these critical vertices were already assigned
and cannot be changed.
values for these critical vertices were already assigned
and cannot be changed.
Considering the subgraph  in Figure 2(c),
a step by step example of the assignment of values to vertices in
in Figure 2(c),
a step by step example of the assignment of values to vertices in  is
presented in Figure 4.
Figure 4(a) presents the initial state of the algorithm.
The critical vertex 8 is the only one that has non-critical vertices as
adjacent.
In the example presented in Figure 3, the addresses
is
presented in Figure 4.
Figure 4(a) presents the initial state of the algorithm.
The critical vertex 8 is the only one that has non-critical vertices as
adjacent.
In the example presented in Figure 3, the addresses  were not used.
So, taking the first unused address
were not used.
So, taking the first unused address  and the vertex
and the vertex  ,
which is reached from the vertex
,
which is reached from the vertex  ,
,  is set
to
is set
to  , as shown in Figure 4(b).
The only vertex that is reached from vertex
, as shown in Figure 4(b).
The only vertex that is reached from vertex  is vertex
is vertex  , so
taking the unused address
, so
taking the unused address  we set
we set  to
to  ,
as shown in Figure 4(c).
This process is repeated until the UnAssignedAddresses list becomes empty.
,
as shown in Figure 4(c).
This process is repeated until the UnAssignedAddresses list becomes empty.
 |
| Figure 4: Example of the assignment of values to non-critical vertices. |
The Heuristic
We now present an heuristic for BMZ algorithm that
reduces the value of  to any given value between 1.15 and 0.93.
This reduces the space requirement to store the resulting function
to any given value between
to any given value between 1.15 and 0.93.
This reduces the space requirement to store the resulting function
to any given value between  words and
words and  words.
The heuristic reuses, when possible, the set
of
words.
The heuristic reuses, when possible, the set
of  values that caused reassignments, just before
trying
values that caused reassignments, just before
trying  .
Decreasing the value of
.
Decreasing the value of  leads to an increase in the number of
iterations to generate
leads to an increase in the number of
iterations to generate  .
For example, for
.
For example, for  and
and  , the analytical expected number
of iterations are
, the analytical expected number
of iterations are  and
and  , respectively (see [2]
for details),
while for
, respectively (see [2]
for details),
while for  the same value is around 2.13.
the same value is around 2.13.
Memory Consumption
Now we detail the memory consumption to generate and to store minimal perfect hash functions
using the BMZ algorithm. The structures responsible for memory consumption are in the
following:
- Graph:
- first: is a vector that stores cn integer numbers, each one representing
the first edge (index in the vector edges) in the list of
edges of each vertex.
The integer numbers are 4 bytes long. Therefore,
the vector first is stored in 4cn bytes.
- edges: is a vector to represent the edges of the graph. As each edge
is compounded by a pair of vertices, each entry stores two integer numbers
of 4 bytes that represent the vertices. As there are n edges, the
vector edges is stored in 8n bytes.
- next: given a vertex
 , we can discover the edges that
contain
, we can discover the edges that
contain  following its list of edges,
which starts on first[
following its list of edges,
which starts on first[ ] and the next
edges are given by next[...first[
] and the next
edges are given by next[...first[ ]...]. Therefore, the vectors first and next represent
the linked lists of edges of each vertex. As there are two vertices for each edge,
when an edge is iserted in the graph, it must be inserted in the two linked lists
of the vertices in its composition. Therefore, there are 2n entries of integer
numbers in the vector next, so it is stored in 4*2n = 8n bytes.
]...]. Therefore, the vectors first and next represent
the linked lists of edges of each vertex. As there are two vertices for each edge,
when an edge is iserted in the graph, it must be inserted in the two linked lists
of the vertices in its composition. Therefore, there are 2n entries of integer
numbers in the vector next, so it is stored in 4*2n = 8n bytes.
- critical vertices(critical_nodes vector): is a vector of cn bits,
where each bit indicates if a vertex is critical (1) or non-critical (0).
Therefore, the critical and non-critical vertices are represented in cn/8 bytes.
- critical edges (used_edges vector): is a vector of n bits, where each
bit indicates if an edge is critical (1) or non-critical (0). Therefore, the
critical and non-critical edges are represented in n/8 bytes.
- Other auxiliary structures
- queue: is a queue of integer numbers used in the breadth-first search of the
assignment of values to critical vertices. There is an entry in the queue for
each two critical vertices. Let
 be the expected number of critical
vertices. Therefore, the queue is stored in 4*0.5*
be the expected number of critical
vertices. Therefore, the queue is stored in 4*0.5* =2
=2 .
.
- visited: is a vector of cn bits, where each bit indicates if the g value of
a given vertex was already defined. Therefore, the vector visited is stored
in cn/8 bytes.
- function g: is represented by a vector of cn integer numbers.
As each integer number is 4 bytes long, the function g is stored in
4cn bytes.
Thus, the total memory consumption of BMZ algorithm for generating a minimal
perfect hash function (MPHF) is: (8.25c + 16.125)n +2 + O(1) bytes.
As the value of constant c may be 1.15 and 0.93 we have:
+ O(1) bytes.
As the value of constant c may be 1.15 and 0.93 we have:
| c |
 |
Memory consumption to generate a MPHF |
| 0.93 |
0.497n |
24.80n + O(1) |
| 1.15 |
0.401n |
26.42n + O(1) |
| Table 1: Memory consumption to generate a MPHF using the BMZ algorithm. |
The values of  were calculated using Eq.(1) presented in [2].
were calculated using Eq.(1) presented in [2].
Now we present the memory consumption to store the resulting function.
We only need to store the g function. Thus, we need 4cn bytes.
Again we have:
| c |
Memory consumption to store a MPHF |
| 0.93 |
3.72n |
| 1.15 |
4.60n |
| Table 2: Memory consumption to store a MPHF generated by the BMZ algorithm. |
Experimental Results
CHM x BMZ
Papers
- F. C. Botelho, D. Menoti, N. Ziviani. A New algorithm for constructing minimal perfect hash functions, Technical Report TR004/04, Department of Computer Science, Federal University of Minas Gerais, 2004.
- F. C. Botelho, Y. Kohayakawa, and N. Ziviani. A Practical Minimal Perfect Hashing Method. 4th International Workshop on efficient and Experimental Algorithms (WEA05), Springer-Verlag Lecture Notes in Computer Science, vol. 3505, Santorini Island, Greece, May 2005, 488-500.
Enjoy!
Davi de Castro Reis
Djamel Belazzougui
Fabiano Cupertino Botelho
Nivio Ziviani

 , where
, where  is in
one-to-one correspondence with the key set
is in
one-to-one correspondence with the key set  for which we wish to
generate a minimal perfect hash function.
The two main differences between BMZ algorithm and CHM algorithm
are as follows: (i) BMZ algorithm generates random
graphs
for which we wish to
generate a minimal perfect hash function.
The two main differences between BMZ algorithm and CHM algorithm
are as follows: (i) BMZ algorithm generates random
graphs  with
with  and
and  , where
, where  ,
and hence
,
and hence  necessarily contains cycles,
while CHM algorithm generates acyclic random
graphs
necessarily contains cycles,
while CHM algorithm generates acyclic random
graphs  with
with  and
and  ,
with a greater number of vertices:
,
with a greater number of vertices:  ;
(ii) CHM algorithm generates order preserving minimal perfect hash functions
while BMZ algorithm does not preserve order. Thus, BMZ algorithm improves
the space requirement at the expense of generating functions that are not
order preserving.
;
(ii) CHM algorithm generates order preserving minimal perfect hash functions
while BMZ algorithm does not preserve order. Thus, BMZ algorithm improves
the space requirement at the expense of generating functions that are not
order preserving.
 is a universe of keys.
Let
is a universe of keys.
Let 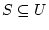 be a set of
be a set of  keys from
keys from  .
We make use of two auxiliary random functions
.
We make use of two auxiliary random functions  and
and  ,
where
,
where  for some suitably chosen integer
for some suitably chosen integer  ,
where
,
where  .We build a random graph
.We build a random graph  on
on  ,
whose edge set is
,
whose edge set is  . There is an edge in
. There is an edge in  .
The vertices and edges in
.
The vertices and edges in  and
and  .
Moreover, we let
.
Moreover, we let  be the set of non-critical
vertices in
be the set of non-critical
vertices in  be the set of all critical
vertices that have at least one non-critical vertex as a neighbour.
Let
be the set of all critical
vertices that have at least one non-critical vertex as a neighbour.
Let  be the set of non-critical edges in
be the set of non-critical edges in  be the non-critical subgraph
of
be the non-critical subgraph
of  corresponds to the acyclic part
of
corresponds to the acyclic part
of  .
.
 of the vertices
of
of the vertices
of  for each
for each  in such
a way that
in such
a way that  (
( ) is a
minimal perfect hash function for
) is a
minimal perfect hash function for  can be found in linear time
if the number of edges in
can be found in linear time
if the number of edges in  (see
(see  .
.
 are constructed as follows.
We impose some upper bound
are constructed as follows.
We impose some upper bound  on the lengths of the keys in
on the lengths of the keys in  (
( ,
,  ), we generate
an
), we generate
an  table of random integers
table of random integers  .
For a key
.
For a key  and
and  , we let
, we let

 for some
for some  in this case.
If we still find a loop after this, we generate another pair
in this case.
If we still find a loop after this, we generate another pair  .
When a multiple edge occurs we abort and generate a new pair
.
When a multiple edge occurs we abort and generate a new pair  .
The crucial step now is to determine the value
of
.
The crucial step now is to determine the value
of  (in
(in  .
Botelho, Menoti an Ziviani determinded emprically in
.
Botelho, Menoti an Ziviani determinded emprically in  .
.
 .
For the example shown in Figure 2(a),
.
For the example shown in Figure 2(a),  after the initialization step.
after the initialization step.

 from the queue, decrement its degree and
the degree of the vertices with degree greater than 0 in the adjacent
list of
from the queue, decrement its degree and
the degree of the vertices with degree greater than 0 in the adjacent
list of  .
At this point, the adjacencies of
.
At this point, the adjacencies of  we collect all
vertices
we collect all
vertices  with at least one vertex
with at least one vertex  that
is in Adj
that
is in Adj and in
and in  , as the vertex 8 in Figure 2(c).
, as the vertex 8 in Figure 2(c).
 such that
the function
such that
the function  defined by
defined by

 to
to  (recall
(recall  ).
We are interested in a labelling
).
We are interested in a labelling  and
and 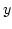 are keys
in
are keys
in  ; that is, if we associate
to each edge the sum of the labels on its endpoints, then these values
should be all distinct.
Moreover, we require that all the sums
; that is, if we associate
to each edge the sum of the labels on its endpoints, then these values
should be all distinct.
Moreover, we require that all the sums  (
( and
and  , and thus we have a bijection
between
, and thus we have a bijection
between  bit value for each vertex
bit value for each vertex  would create two edges with the same sum,
we try
would create two edges with the same sum,
we try  for
for  be the set of addresses assigned to edges in
be the set of addresses assigned to edges in  .
Initially
.
Initially  .
Let
.
Let  .
Considering the subgraph
.
Considering the subgraph  in Figure 3(a) is
chosen, the assignment
in Figure 3(a) is
chosen, the assignment  is made and
is made and  .
.

 all adjacencies
of vertex
all adjacencies
of vertex  .
Next, for all
.
Next, for all  , we check if
, we check if  .
Since
.
Since  , then
, then  is set
to
is set
to  ) and
) and  .
Next, vertex
.
Next, vertex  is reached,
is reached,  is set
to
is set
to  .
Next, vertex
.
Next, vertex  is reached and
is reached and  .
Since
.
Since  and
and  , then
, then  is
set to
is
set to  .
Finally, vertex
.
Finally, vertex  is reached and
is reached and  .
Since
.
Since  ,
,  ,
,  and
and  , then
, then  is set
to
is set
to  and
and  . This finishes the algorithm.
. This finishes the algorithm.
 were not used.
So, taking the first unused address
were not used.
So, taking the first unused address  is set
to
is set
to  , as shown in Figure 4(b).
The only vertex that is reached from vertex
, as shown in Figure 4(b).
The only vertex that is reached from vertex  to
to  ,
as shown in Figure 4(c).
This process is repeated until the UnAssignedAddresses list becomes empty.
,
as shown in Figure 4(c).
This process is repeated until the UnAssignedAddresses list becomes empty.

 words and
words and  words.
The heuristic reuses, when possible, the set
of
words.
The heuristic reuses, when possible, the set
of  and
and  , the analytical expected number
of iterations are
, the analytical expected number
of iterations are  and
and  , respectively (see
, respectively (see  the same value is around 2.13.
the same value is around 2.13.
 be the expected number of critical
vertices. Therefore, the queue is stored in 4*0.5*
be the expected number of critical
vertices. Therefore, the queue is stored in 4*0.5*